Dip and rise today, will 6591 hold?

Good morning, as expected a bit of a hard one to read yesterday, and a theme that will probably continue for most of this week as people start to gear up for the QE news on Wednesday and possible tapering. It feels like an approximately $10bn cut per month is priced in now as indices all held up pretty well yesterday, though gave up some of the gains made on the news that the Fed nominee Summers has withdrawn. The UK government are finally selling part of their Lloyds holding after 5 years, with strong demand from the US apparently for the shares, at around 75p per share.

Unfortunately the FTSE didn’t quite reach my upper target yesterday at 6670 where the short order was waiting but not to worry, better than trying to second guess with a choppy market. It might be a bit clearer today before it gets volatile tomorrow. Overall the FTSE held up well yesterday and maintained the gains on the news driven rally. That rise may well continue for a little longer, but will need to break 6652 to possibly see the 6672 mentioned yesterday.

Asia Overnight from Bloomberg

Oil slid for a third day as the threat of military strikes against Syria receded. Emerging-market currencies weakened and Asian stocks declined before the U.S. Federal Reserve’s policy meeting.  U.S. Secretary of State John Kerry joined top French and U.K. diplomats in calling for a United Nations resolution to eliminate Syria’s chemical arsenal, with the ultimate goal of forcing President Bashar al-Assad from power. The Federal Open Market Committee meets today and tomorrow, when members are forecast to cut monthly bond buying by $10 billion to $75 billion. A U.S. government report today is expected to show the annual increase in the cost of living slowed in August.

“The Syrian situation is contributing to these softer prices,” said Michael McCarthy, chief market strategist at financial derivatives dealer CMC Markets in Sydney. “It’s quite clear now we have a path out of the current dilemma, with the U.S. saber rattling and potential for a military strike receding.”

U.S. Futures

Standard & Poor’s 500 Index futures slipped 0.1 percent, contracts on natural gas gained a fourth day and agricultural commodities advanced.

The FOMC will probably cut monthly purchases of Treasuries to $35 billion from $45 billion and keep mortgage-bond buying at $40 billion at the meeting starting today, according to a Bloomberg News survey of economists earlier this month.

“The market consensus is that the Fed will decide to trim its quantitative easing, but investors don’t want to shift their positions one way or the other before the key event,” said Takahiro Nakano, a Tokyo-based senior strategist at Mizuho Trust & Banking Co., a unit of Japan’s third-largest bank by market value.

Fed Leader

Global stocks surged to a five-year high yesterday after Lawrence Summers withdrew as a candidate for the position of Fed chairman. The S&P 500 Index closed 0.6 percent higher after rallying as much as 1 percent.

Summers, a former Treasury secretary, would have tightened central bank policy more than Fed Vice Chairman Janet Yellen, who was his main rival to replace Chairman Ben S. Bernanke, according to a Bloomberg Global Poll conducted last week. Bernanke’s term as Fed chairman ends on Jan. 31.

Outlook

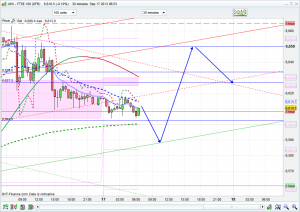
ftse 100 prediction
ftse 100 prediction

I have a couple of supports at 6590 now, namely the bottom of the 10 day Bianca and Raff channels, as well at 6599 being the gap close on the chart from Fridays close. The trend is still up, QE tapering in some form is probably priced in so a long around this level could be a decent trade. I have drawn the arrows to that effect as the 30 minute channel also has support there. As mentioned above with the S&P and Dow not far off supports (and the Dax come to that) we do have some decent support levels. As mentioned this won’t be the easiest week to trade, especially tomorrow, as I am sure we will see a few rumour driven spikes/movements. For today I expect a dip down to that 6590 level and then hopefully a nice bounce back to the 6650 area. If that breaks then we should get 6672 but probably not much more, as the Bianca channels still have the top around the 6650/60 area. Basically a long around 6590 looks ok, a short around 6650 looks ok. The channel bands are narrowing which isn’t surprising as indices get ready to spring out one way or the other once the QE situation is clarified.

37 Comments

  2. It looks like a second day of sell. Do you think long may happen after 13.00? I see a double bottom at the moment. But looks very weak.

  4. FTSE and NASDAQ have given up the gains over last Friday’s close due to the Summers gap up, as NR169 (I think) predicted. The Dow and S&P 500 are hanging on to some of the increase in each case. Tomorrow’s Fed announcements have the potential to disrupt, otherwise, I’m still expecting a flat to slightly negative bias for the FTSE for the remainder of the week.

  5. I am a simple chap and to that end have been very happy with Tradefair and FinSpreads (back up platform) as my two providers. Now Tradefair are changing provider and have launched Tradefair Plus. I transferred yesterday and am hating the new platform.

    So not concentrating on trade opportunities as I should be.

    Not in any way surprised that the FTSE has settled back. As I stated yesterday. In the NHS Consultants dont tend to be at the coal face during all out of hours timeframes. Senior market makers are the same. That is why we often see over reactions to news events at weekends.

    Now I am looking for two bits of advice.

    1. What are the platforms of choice for traders here.

    2. despite being full time for well over two years I have never been able to get my head around using Calls and Puts as part of my trading strategies. Can anybody enlighten me as to how to make use of them.

    Keep the stops in

    Safe trading

    2. Given that you are already trading CFDs Options can be used to trade volatility, ie making money is not dependent on market direction but whether it trades without or outside a range. However for retail customers the implied vols are marked so high that basic option strategies like straddles become too costly to be worthwhile. Instead brokers prefer customers to have outright punts as most options expire worthless.

      An alternative strategy would be writing options on physical shares you already hold. You could sell otm call options on your equities – collecting additional cash premiums. If the option expires itm then you can sell your shares (at a profit).

      There are numerous ways options can be used but it depends on your objectives and means.

    3. To my mind there is no reason at all why electronic execution of a transaction should not be instantaneous. Perhaps there are practical problems to do with displaying price values at the same frequency as that delivered by the data feed. If so, there might be a case for SBs (:)) to disallow transactions if the difference between the displayed price and the actual price is to the disadvantage of the SB. Unfortunately, as so often, what seems like a reasonable provision could easily change into thoroughgoing abuse of the punter. E.g. by waiting until the price moves to the SB’s advantage before accepting the bet.

      Does anyone have intimate knowledge of this area? Any such conditions should be transparent and explained to the customer.

      At any rate I have no complaints about the speed of execution offered by IG.

  7. No long Jack! I am short since yesterday from 6650 and looking for 6500 at some point this week. If I will have it then I’m done for the month

  9. May worth to short Nasdaq right after opening with a tight stop last week and yesterday it dropped nearly every day, a few times well over 100 pips

  11. Bee considering my luck, I`ll do just that and it will go against me. But yeah thanks for the heads up, might try that with low volume as I have noticed that but didn`t want to get on the wrong side of it.

  12. What an idiot me, came out 6598 because I was such a slow start and I was so scared it won’t go through 6600 and plus because of being too brave yesterday when my 20 points just slipped out my hands and I got even -10 instead. Plus because I lost 7 points in the morning. Gosh, I wanted to take those money. But I would be winning another 7 on top at the moment and who knows how much more I will miss. It’s always like this, when I am brave, it doesn’t work, when I am too cautious it works against me.

      1. 7.2 points profit for today, I should be positive, it’s not a loss of 4 points like yesterday. I will try another day and maybe I would be more lucky.
        But the entry was 6587.5. So annoyed.

        1. What annoys me even more that I am still -10 points from where I started back at the beginning of September. I am breaking even from the beginning of the month and can do nothing about it.
          I have good entries – bad exits. I have also impatient entries and lots of closures with losses and brings all the rare wins to break even. I need a break of at least 60 points. I just dream about those 60 points. I need it.

  13. I still believe that ftse will end positively by 4:30. Unlike you Jack I still have my long running -`O ye of little faith`

      1. As a day trader there was always the possibility to change tac. Sometimes the market goes against you, but I would be wary being too bearish as well this week, either way I got 15 points on the drop. Though 30-40 points isn`t something to celebrate about, the market is still in a very strong UPtrend.

      1. LOL, was a bit over optimistic eh! Going to be tricky this week all week! Just one trade today, long at 6591…. got a few…

  16. A bit of relief for the likes of me. Next key level is 6550. Should be testing 6517 within a couple of days.

  17. …. the true story playing out here is there is going to be no change in the QE plan, steady as she goes got to be worth an hysterical 1% plus move when its announced … all indicies 🙂

  18. jack you were lucky to get out when you did…….had long on ftse at 6600 stoped out at 6570 20 per point back in long at 6580 maybe not a wise move losed a lot this week trying to recover some back

    1. It looks like this, john. I came out at 6598 and called it a day and didn’t look at charts until now. I expected it to be at 6650 or something and was very surprised.
      However at 15.00 I noticed that the top didn’t go higher than the previous high at 10.00 so it made my cautions to reopen the long when it actually came down to 6598 again.
      (the pattern on 1 min chart reminded me a “Christmas tree” pattern which I called myself when experienced it first time on DAX: Bernanke gave a speech on 5.07.13. It went down -170 points after that spike, not easy to forget and I also recorded my crying and praying on the video, which is a remarkable recording. When I want to remind myself of stop losses – I watch that video and that puts me off avoiding stop losses a big time!)

  19. Well john we might see the rise in the morning as s&p is climbing in ftse sfter hoursso im sure we will see that in the morning

Comments are closed.